差分法で二階放物型偏微分方程式を解けばいいだけ～（2009年10月9日公開分）

いいだけなんですが、タスクとしてはでかいです(汗)

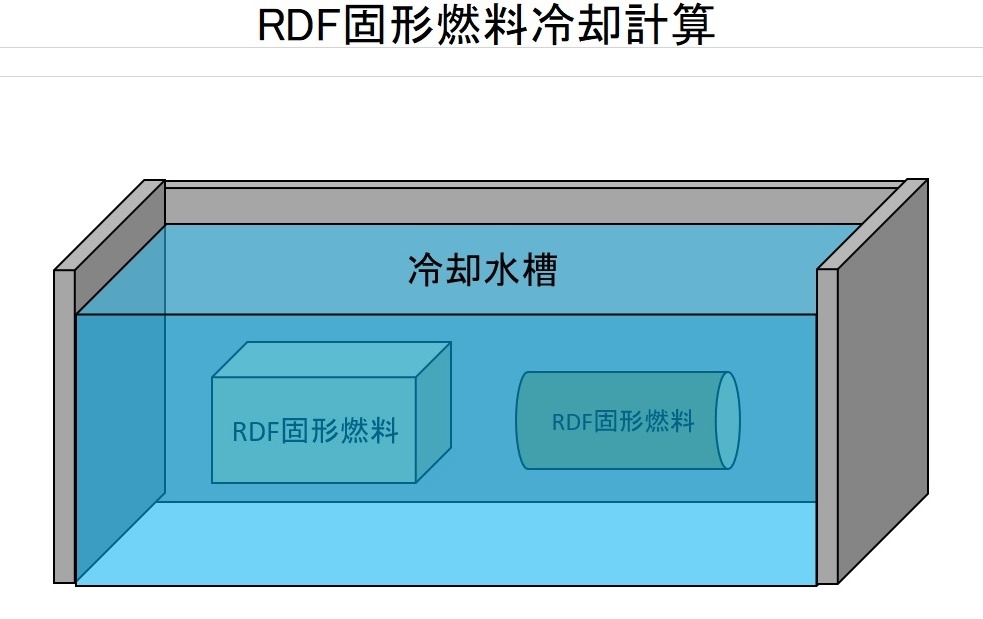
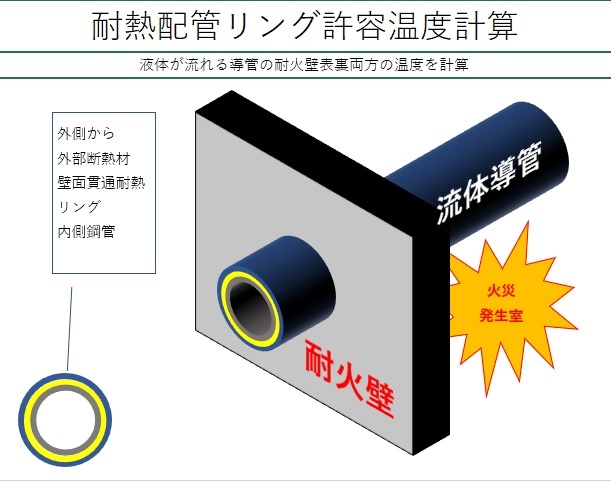
先日、一次元の非定常熱伝導を解かないと回答できない案件があり、しかもこの案件は均質な物質内の温度変化でなく、多層平板でした。

おそらく、CAEが無かったころの方は図式解法で解いていたのでしょうけど、各種書籍には、その具体的手法が載っておらず、力づくで差分法によるプログラムを組もうと思いました。

早い話、下の式達を解ければ、多層だろうが、何層の平板であれ、任意場所、任意時間の温度は求まります。

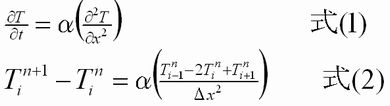
均質な平板で、境界条件が熱伝達面の場合は、式(1)を変数分離法で解いた解析解があります。

(これも、フーリエ級数を含むので、プログラムを組む必要がありますが。。。。)